Hodrick -Prescott
Hodrick -Prescott는 시계열 데이터에서 경향성과 순환성을 분리하는데 주로 사용된다. 다음은 hp필터를 사용해 트랜드와 사이클을 분리하고 트랜드와 실제 gdp 비교한 그래프이다.

ETS Models
오차(E), 추세(T), 계절성(S) 지수평활법, 추세모형과 같은 다양한 모델을 포함하지만 ETS 분해에 대해 알아보자
각각의 요소들을 더하거나 곱하는 등 요소의 기반에 데이터에 맞는 일반화 모델을 만들 수 있다.
* 덧셈모델 : 추세가 선형에 가깝고 계절성이 일정할때
* 곱셈모델 : 매년 승객수가 전년에 비해 증가하는 지수형일때
ETS분해
승객수의 시계열 데이터를 다음과 같이 분석해보자. 결측값음 dropna를 사용하여 처리하였고, 지수형으로 판단하여 Multiplicative로 모델링 하였다.

위와같이 seasonal_decompose를 사용하여 데이터를 분해하였고 맨위가 원시 데이터, 아래가 Trend, Seaonal, Residual을 나타낸다. 따라서 위 그래프를 통해 경향와, 계절성, 잔차를 분류함으로써 선형인지 지수형인지 잘 확인할 수 있다.
EWMA Models
지수가중 이동 평균 -> 단순이동평균의 단점을 보안(rolling)
단순이동 평균(SMA)의 단점
1. 이동 평균기간이 짧아질수록 시계열 데이터를 더 잘 설명할 수 있지만 잡음이 큼
2. 이동 평균 기간만큼 시차가 생김
3. 이동 평균 기간이 짧더라도 극대값과 극소값에 미치지 못함
4. 미래변동에 정보가 없어 그냥 추세만 보여줌
5. 극단적인 데이터는 단순이동 평균을 왜곡시켜 부정확
EWMA: 최근의 값에 가중치를 적용해 시차 효과를 감소

위와 같이 계절성의 추세가 최근일수록 더 잘 나타나는데 이는 최신의 자료에 더 큰 가중치를 두었기 때문이다. 다음은 EMMA에 관한 일반식이다.
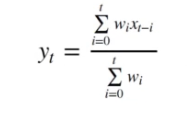
이때 w는 가중치를 의미하며 이는 ewm()매소드로 정할 수 있다. 만약 adjust가 True일때

와 같이 가중치가 계산되며 이는 아래와 같이 최근에 가까워질수록 가중치가 증가함을 확인할 수 있다.

adjust가 False일 경우 다른 방법으로 계산되며 이는 span, center of mass, halflife등으로 결정된다.
Holt- Winters model
지수평활법 + 계절설기법
->3개의 평활식 수준(l_t),추세(b_t),계절성(s_t)
각각에 대응하는 알파,베타,감마를 갖는다
이 방법은 계절성 요소의 성질에 따라 두가지로 바뀔수 있음
- 덧셈기법:계절적 변동폭이 데이터의 수준과 일정하게 나타날때
- 곱셈기법:계절적 변동폭이 데이터의 수준에 비례하여 나타날때
단일 지수평활법 (Single Exponential Smoothing)

이때 α는 평활 계수로 현재 관측치에 얼마나 높은 가중치를 가한건지를 결정한다.

위와 같이 단일지수평활법을 이용해서 모델링을 할 수 있다. 위와 같이 모델을 만들고 피팅을 해주면 모델링 작업이 끝난다.
이중 지수평활법 (Double Exponential Smoothing)
추세와 경향이 있는경우 사용되는 모델로 단일지수평활법에 추세 평활계수 β가 추가되어 예측한다.

이중지수 평활법은 trend에 대한 선형성, 지수성을 따져야 하기에 두 그래프 모두 출력해보았다. 아래 그래프를 보면 원시데이터가 DES_add_12와 거의 일치함을 확인할수 있다. 따라서 이 데이터는 선형성이라고 말할 수 있다.

삼중 지수평활법 (Triple Exponential Smoothing)
이중지수평활법에서 계절성을 포함하는 새로운 평활계수 γ가 추가된다.
airline['TES_mul_12'] = ExponentialSmoothing(airline['Thousands of Passengers'],trend='add',seasonal='mul',seasonal_periods=12).fit().fittedvalues
airline['TES_add_12'] = ExponentialSmoothing(airline['Thousands of Passengers'],trend='add',seasonal='add',seasonal_periods=12).fit().fittedvalues삼중 지수 평활법의 경우 seasonal에 대한 덧셈,곱셈모형을 따져줘야 하고, 이에 따른 주기도 설정해주어야 한다. trend는 add모형을 사용하고 seasonal역시 두 모델을 만들어 비교해보았다.
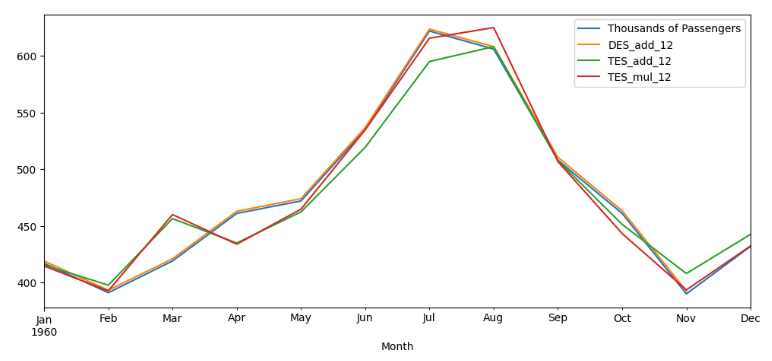
그래프를 확인하면 삼중시수평활법이 이중지수평활법보다 성능이 떨어짐을 확인할 수 있다. 더 고차원적인 삼중지수평활법이 예측의 정확성이 더 떨어지는 이유는 계절적 변동까지 고려했기 때문이다. 하지만 삼중지수 평활법은 데이터가 많을때 예측 정확도가 올라간다. 위 그래프는 데이터의 시작 1달을 고려한것이고 데이터가 후반으로 갈수록 삼중지수평활법이 더 좋은 성능을 보임음 확인할 수 있다.
다음시간에는 데이터 예측을 위한 여러 모델들을 정리해야겠다.
'PC > 시계열 데이터분석' 카테고리의 다른 글
| 시계열 데이터분석(1) - datetime과 기본 (0) | 2023.08.22 |
|---|
